Jumat, 05 Juni 2020

TURUNAN FUNGSI

TURUNAN FUNGSI

Assalamualaikum wr wb, pada pembahasan kali ini saya akan membahas tentang TURUNAN FUNGSI.

DEFINISI TURUNAN
Turunan fungsi (diferensial) ialah fungsi lain dari suatu fungsi sebelumnya, misalkan fungsi f menjadi menjadi f' yang memiliki nilai tidak beraturan.

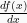Pada fungsi y = f(x), turunan dari variabel y terhadap variabel x dinotasikan dengan \frac{dy}{dx} atau \frac{df(x)}{dx} atau y' dan didefinisikan sebagai : 
f'(x) =\lim\limits_{h\to 0}\frac{f(x+h)-f(x)}{h}

RUMUS - RUMUS TURUNAN FUNGSI ALJABAR
Aturan-aturan dalam turunan fungsi :

1. Rumus Turunan Fungsi Pangkat f(x) = x^n
     Fungsi berbentuk pangkat turunannya dapat menggunakan rumus 
    f'(x) = \lim \limits_{h \to 0}\frac{f(x+h)-f(x)}{h}  sebagai :
    
   Maka, rumus turunan fungsi pangkat adalah 
   f'(x ) = nx^{n-1}

2. Rumus Turunan Hasil Kali Fungsi 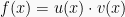 f(x) = u(x) \cdot v(x)
    Fungsi f(x) yang terbentuk dari perkalian fungsi u(x) dan v(x), turunannya didapat
    dengan :
   
    Maka, rumus turunan fungsinya adalah 
    f'(x)=u'v+uv'

3. Rumus Turunan Fungsi Pembagian  f(x)=\frac{u(x)}{v(x)}
    f'(x) = \lim \limits_{h\to0}\frac{f(x+h)-f(x)}{h}\overset{menjadi}{\rightarrow}\lim \limits_{h\to0}\frac{\frac{u(x+h)}{v(x+h)} - \frac{u(x)}{v(x)}}{h}
    sehingga :
    Maka, rumus turunan fungsinya adalah 
   f'(x) = \frac{u'v-uv'}{v^2}

4. Rumus Turunan Pangkat dari Fungsi 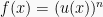f(x)=(u(x))^n
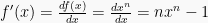
     Jika f(x) = x^n , maka f'(x)=\frac{df(x)}{dx}= \frac{dx^n}{dx} = nx^n-1

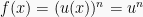     Karena f(x) = (u(x))^n=u^n , maka
    f'(x) = \frac{df(x)}{dx} = \frac{du^n}{dx} \cdot \frac{du}{du}  atau  f'(x) = \frac{du^n}{du} \cdot \frac{du}{dx} = nu^{n-1} \cdot u'

     Maka, rumus turunan fungsinya adalah 
    f'(x) = nu^(n-1) \cdot u'


RUMUS - RUMUS TURUNAN FUNGSI TRIGONOMETRI
Berdasarkan definisi turunan, dapat diperoleh rumus-rumus turunan trigonometri yaitu sebagai berikut : (dengan u dan v masing-masing fungsi dari x)

CONTOH SOAL :
1.  Turunan pertama dari 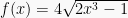f(x) = 4 \sqrt{2x^3 - 1} adalah
     jawab :
     Soal ini merupakan fungsi yang berbentuk y=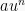au^n yang dapat diselesaikan dengan
     menggunakan rumus 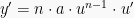y' = n \cdot a \cdot u^{n-1} \cdot u', maka f(x) = 4 \sqrt{2x^3-1} = 4(2x^3-1)^{\frac{1}{2}}
      Sehingga turunannya :
  

2.  Tentukan turunan pertama dari
     f(x) = \frac{6}{\sqrt[3]{\sin (3x-\frac{\pi}{5})}}
      jawab :
     Untuk menyelesaikannya kita gunakan rumus campuran f'(x) = \frac{u'v-uv'}{v^2} dan 
     y' = n \cdot u' \sin^{n-1}u \cdot \cos u  
      Sehingga turunannya :
 






Demikian hasil resume saya tentang TURUNAN FUNGSI. Semoga dapat bermanfaat.
Sekian dan terimakasih. Wassalamualaikum wr wb.



Diposting oleh di

Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)